一,容斥原理
设S是一个集合,Ai 是S 中具有性质 Pi 的元素组成的子集合。那么,S中既不具有性质P1,也不具有性质P2,...更不具有性质Pn 的元素个数为:

二,容斥原理计算 有限制的重组合问题
①什么是有限制的重组合问题?(重组合就是,某个元素可重复选择)
从集合{k1·b1,k2·b2,....,kn·bn}中选取r个元素,(不考虑次序),一共有多少种组合?
元素,可以是一个抽象的概念。一切问题,只要满足这个“范式”,就可以视为一个重组合问题,从而用容斥原理求解。
从集合可以看出:b1最多只能选取k1个,b2最多只能选取k2个,...,bn 最多只能选取kn个
而在的末尾提到了无限的重组合问题求解公式。因此,可以试着将有限制的重组合问题转化为无限制的重组合问题(但是附加了一些条件)。
解法如下:
首先考虑问题1:在无限制的重组合问题的 集合中选取 r 个元素时,一共有多少种选取方法?----答案是一共有F(n,r)种。
然后再定义: 性质A1 表示 问题1得到的选取方案中 至少要存在 k1+1 个b1
性质A2 表示 问题1得到的选取方案中 至少要存在 k2+1 个b2
.....
性质An 表示 问题1得到的选取方案中 至少要存在 kn+1 个bn
从而,问题:从集合{k1·b1,k2·b2,....,kn·bn}中选取r个元素,(不考虑次序),一共有多少种组合?
转化成了:从集合{∞·b1,∞·b2,....,∞·bn}中选取r个元素,(不考虑次序),并且b1不超过k1 b2不超过k2,bn不超过kn,一共有多少种组合?
因此,有限制的重组合问题就转化成了无限制的重组合问题,但是附加了条件:b1不超过k1 ,b2不超过k2,bn不超过kn
用数学公式表示就是:|A¯1 ∩ A¯2∩....A¯n| A¯1表示不具有A1性质的集合(即A1的非)
根据容斥原理:|A¯1 ∩ A¯2∩....A¯n|就可以计算出来了。
三,容斥原理计算错排问题
错排问题就是:给定N个数1,2,3...n 要求第 i 个数不在 第 i 个位置上,一共有多少种排列?
性质A1表示第 1 个数恰好在 1 位置上
性质A2表示第 2 个数恰好在 2 位置上
.....
性质An表示第 n 个数恰好在 n 位置上
错排问题就可以表示成公式:|A¯1 ∩ A¯2∩....A¯n| ,就可以用“容斥原理”来计算了。
四,棋盘多项式
是一种更复杂度的错排问题。
比如,给定一个4行4列的矩阵,元素1不能放在第1行第2列;元素2不能放在第4行第3列;元素3不能放在第1行第3列。求这三个元素一共有多少种放置方式?
五,母函数
母函数有两种:普通的母函数 和 指数母函数。普通母函数一般用来解决组合问题,指数母函数用来解决排列问题。
不管是排列问题,还是组合问题。都是从 n 个数中选出若干个数。排列问题关注的是:是把选出的数做排列(考虑顺序),组合问题则是不考虑顺序。
①普通母函数
(1+x)(1+x)...(1+x)(1+x)=(1+x)n 这个公式表示了:一共有n个物品,每个物品要么不选,要么选中(每个物品最多只能选一次)。
对于每一项(1+x),1 表示不选,x表示选中。一共有 n 个(1+x),即表示一共有 n 个物品。
那么从 n 个物品中选取 r个一共有多少种选择?(不考虑顺序--默认是组合问题)
将(1+x)(1+x)...(1+x)(1+x) 乘出来,得到1,2...n的多项式。xr 的系数就是: n 个物品中选取 r个的 总共的选取方法数。
由二项式定理:(1+x)n = C(n,0)X0 Yn + C(n,1)X1 Yn-1 +.....+ C(n,n)Xn Y0 = C(n,0)X0 + C(n,1)X1 +.....+ C(n,n)Xn(其中Y=1)
可以看出 xr 的系数为C(n,r),刚好符合。
普通,对这种简单的组合问题,用普通母函数计算太复杂了。普通母函数合适的是更复杂一些的组合问题。
如,有 n 个物品,每个物品最多可选两次,从中选取 r 个有多少种选择方案?母函数为:
(1+x+x2)(1+x+x2).....(1+x+x2) = (1+x+x2)n
选择方案数为(1+x+x2)(1+x+x2).....(1+x+x2) = (1+x+x2)n 的 xr 的系数。
再比如,有 n 个物品,每个只能选奇数次,母函数如下:
(x+x3+...x2k-1)(x+x3+...x2k-1).....(x+x3+...x2k-1) = (x+x3+...x2k-1)n
......
再比如,有4 个物品,第1个物品最多只能选 2次,第二个物品只能选奇数次,第三个物品只能选偶数次,第四个物品最多只能选取3次。从中选取 r 个物品,一共有多少种选择方案?(组合问题)
普通母函数如下:(1+x+x2)(x+x3+...x2k-1)(1+x2+...x2k)(1+x+x2+x3)
将上面的母函数解出来,xr 的系数就是选择的方案的数目。
②指数母函数
指数母函数的用法与普通母函数的用法一致。只不过是“表示形式”不同而已。
(1+x+x2+x3)在普通母函数中 表示某个物品在组合计数中 可选0次,1次,2次,3次【或者说该物品最多可选3次】
那指数母函数中选择某个物品该如何表示呢?
(1+x+x2/2!+x3/3!+...+xk/k!)就表示:某个物品在排列计数中 可选0次,1次,2次....k次【或者说该物品最多可选k次】
如,有 n 个物品,每个物品最多可选两次,从中选取 r 个有多少种选择方案?母函数为:
(1+x+x2/2!)(1+x+x2/2!).....(1+x+x2/2!) = (1+x+x2/2!)n
选择方案数为(1+x+x2/2!)(1+x+x2/2!).....(1+x+x2/2!) = (1+x+x2/2!)n的 xr 的系数。
再比如,有4 个物品,第1个物品最多只能选 2次,第二个物品只能选奇数次,第三个物品只能选偶数次,第四个物品最多只能选取3次。从中选取 r 个物品,一共有多少种选择方案?(排列问题)
指数母函数如下:(1+x+x2/2!)[(x+x3/3!+...x2k-1/(2k-1)!)][(1+x2/2!+...x2k/(2k)!](1+x+x2/2!+x3/3!)
排列的方案数就是指数母函数解出来,xr的系数
六,整数拆分
给定一个整数 n,将 n 拆分成 1,2,3 的和,一共有多少种拆分方式?
比如:n=4。 4=1+1+1+1;4=1+1+2;4=2+2;4=1+3
故一共有4种拆分方式。
考虑(1-x)-1 = (1+x+x2+...+xn),根据上面的普通母函数可知:“某个物品可选0次,1次,2次.....n次” (1*[0,1,2,...n])
比如:x3 就表示数字1选取了3次,x2表示数字1选取了2次....
考虑(1-x2)-1 = (1+x2+x4+...+x2n),根据上面的普通母函数可知:“某个物品可选0次,2次,4次.....2n次” (2*[0,1,2,...n])
比如:x6就表示数字2选取了3次,x4表示数字2选取了2次....
考虑(1-x3)-1 = (1+x2+x4+...+x2n),根据上面的普通母函数可知:“某个物品可选0次,3次,6次.....3n次”(3*[0,1,2,...n])
比如:x6就表示数字3选取了2次,x3表示数字3选取了1次....
因此,整数 n 拆分成1,2,3之和的方式数为:
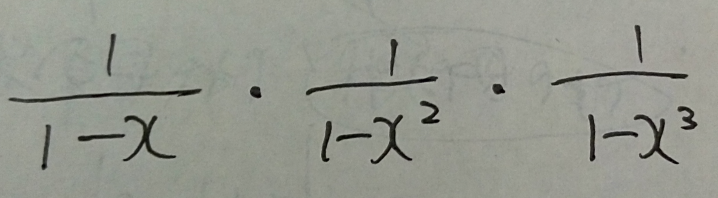
(1-x1)-1 *(1-x2)-1 * (1-x3)-1 的 xn 的系数就是整数 n 拆分成 1,2,3 之和的方式数。(也就是说 n 只能由 1,2,3 相加得到,但是1,2,3,可以出现多次)
定理:给定一个整数 n ,将 n 拆分成 a ,b ,c ...和的方法数是:
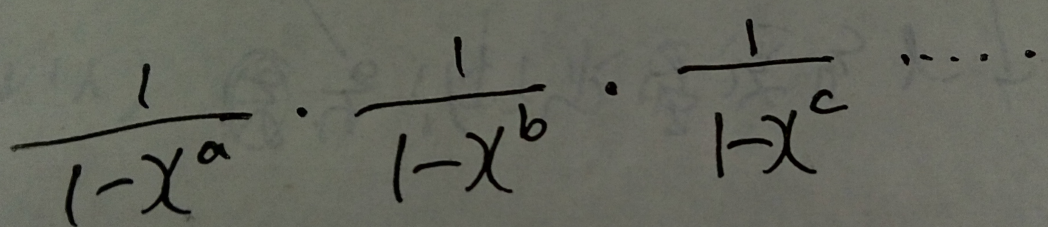
七,一些常用的泰勒展开式
(1-x)-1 = 1+x2+x3+....+xn+...
ex=1+x+x2/2!+x3/3!+...+xn/n!+....
八,参考资料